皆さん こんにちは。
一向にプログが続かない水野です。
すごく久しぶりです。
さて、いわゆる設計者CAEということで入門者向けのCAEセミナーをやることが多いのですが、そのような場合に想定されるのは「線形」の静的応力解析です。
それゆえ、セミナーの中では非線形に関わる話はしません。
実際、そこまで話をしだすと長くなるし、寝る人も増えるし、そもそも時間がないし。
ですが、最近思ったのですが、それでもある程度非線形の話、特に幾何学的非線形の話はしておかなければいけないのじゃないか、と思うようになりました。
まあ、通常、設計という観点からは確かに線形という想定で十分なことは確かです。
とはいえ、自然の物体の挙動はそもそも非線形で、その中のごくごく一部を取り出して線形で考えてよいよ、としているわけです。
で、その範疇に収まっていれば大体問題ないのですが、範囲を逸脱すると突然、解析結果は暴れだします。
ここまでは線形解析でOKよ、とかここから非線形ね、とデジタルで線引ができるわけでなく設計者が、自分で判断する必要があります。
判断のためには知識が必要です。知識がなければ単なる直感になってしまい、甚だ根拠のないことにもなりえます。
例えば、こんな50mm角の正方形の板があって、下のエッジの左端の頂点をピン固定、右端の頂点を上に20mm強制変位をかけるとします。
強制変位をかける右端の頂点はX方向にはフリーにしているので自由に動くことができます。

で、線形解析で解析を実行します。どんな結果を想定するでしょうか。
多分、こんな感じじゃないかと思います。
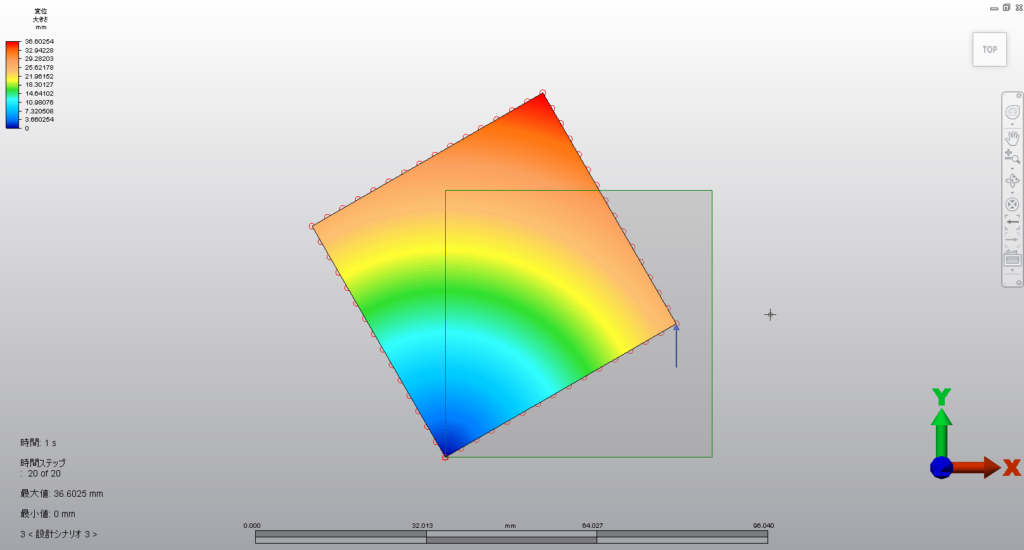
常識的にそうですし、実際、物理的にもそうなるでしょう。
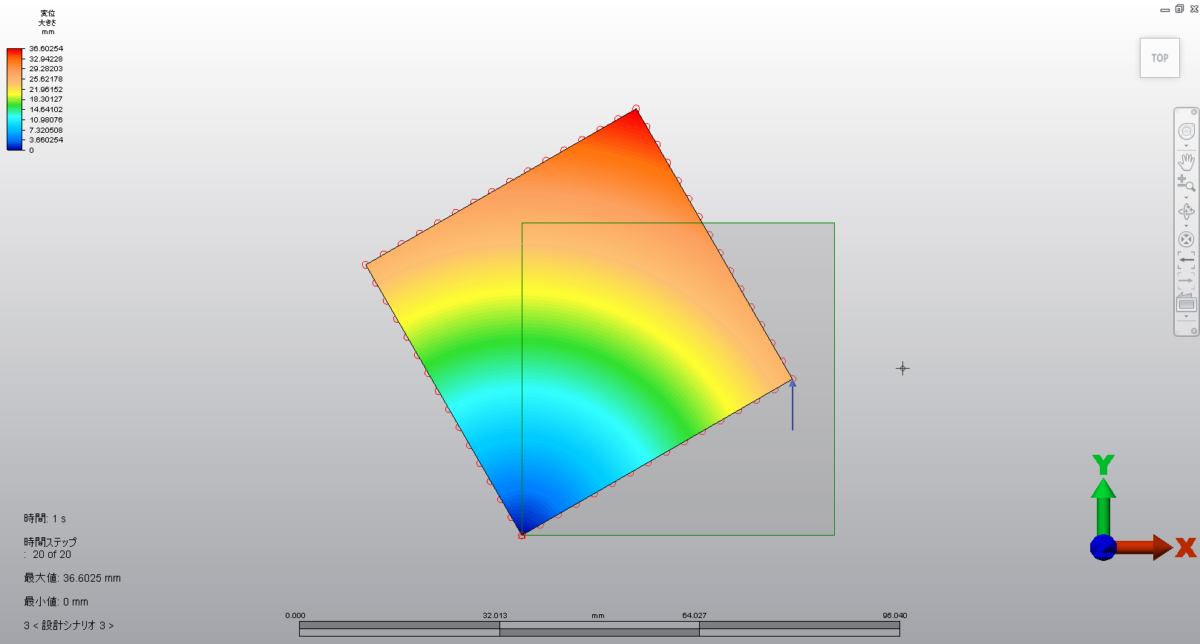
でも、線形応力解析をやるとこうはなりません。
こちらが答えになります。
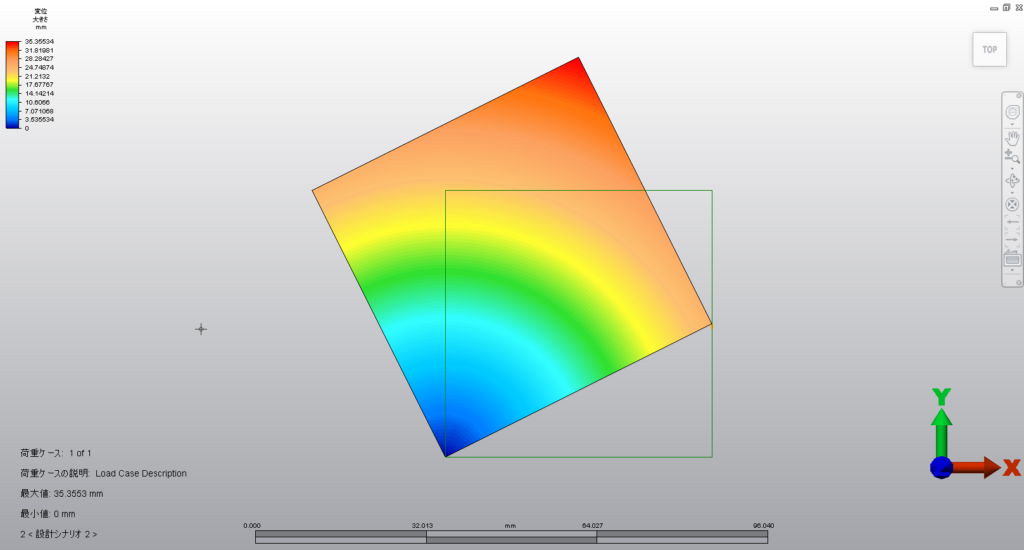
おっと板が拡大しております。
どう考えても変ですよね。
こんなに板が大きくなっているのに(笑)ひずみはほぼゼロです。
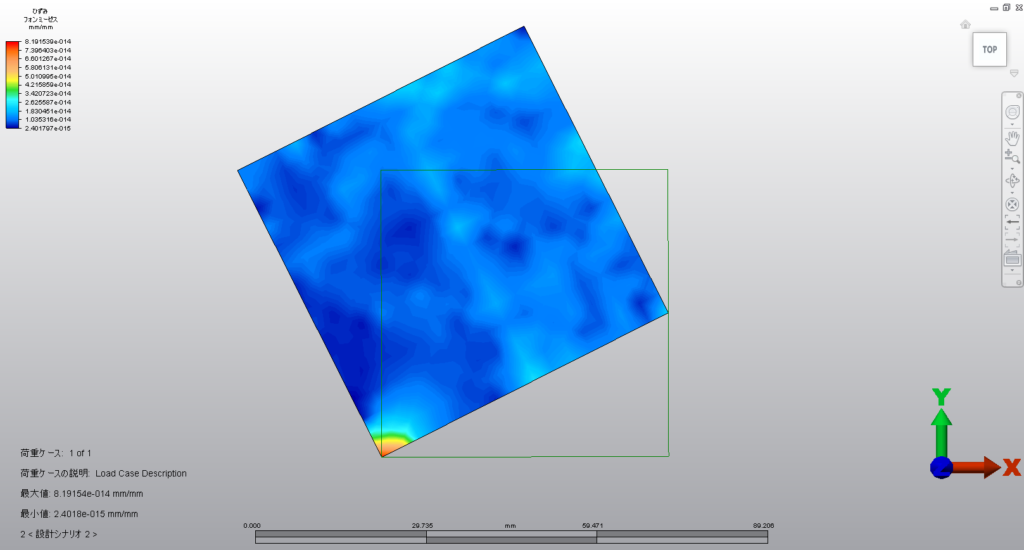
もっとも、これは剛体回転をするので板が変形するわけがなく
したがってひずみがゼロならむしろ正しいでしょう。
こんな摩訶不思議な現象がおきるのが実は線形の応力解析だったりします。
ちなみに、これを非線形解析でやったらどうなるでしょうか?
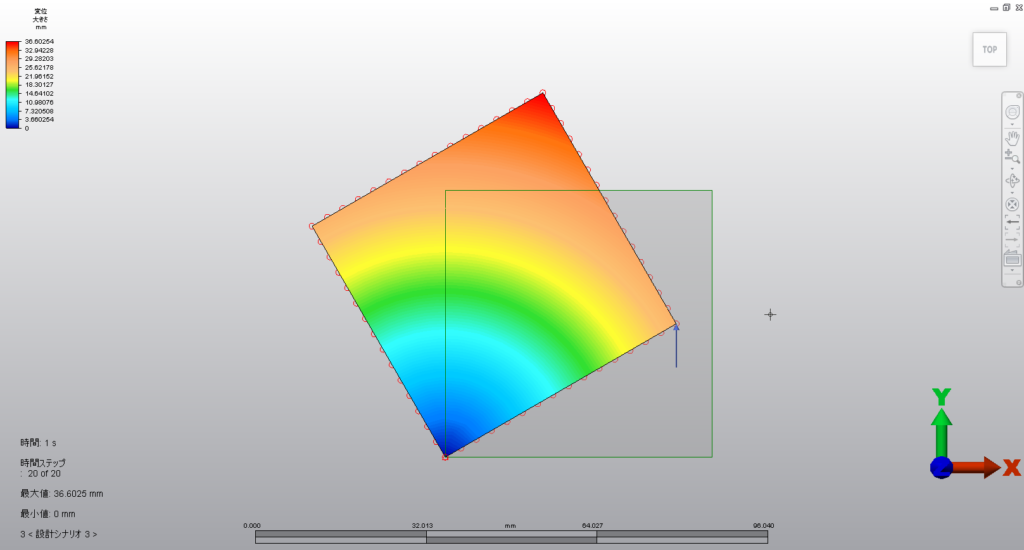
最初の絵と同じですが、現実と合っているようです。
いずれにしてもなんでこんな風に答えが違っちゃうんでしょうか?
本日は、こんな違いがあるよ、ということをお話しするに留めて
次回以降は謎解きをしていこうと思います。
ではでは~